Beating the Doldrums

Strap in, it’s going to be dull. Until suddenly it won’t be

Some quick notes before we get going. What’s Wrong With Democracy is finally coming to the end of our twenty-part series. It’s been a total blast for me, with many thanks to my producers Ada Barume and Eleanor Biggs, and to Jasper Corbett, Katie Gunning and James Harding for thinking of me in the first place. Episodes on climate change here, and AI here, with the final episode on elections later this week. BBC Rethink has seen recent episodes on voting (Glen Weyl, Rosie Cooper, Hannah White, Rob Ford), wealth (Ingrid Robeyns, Sam Dimitriu, Helen Miller and Liam Byrne), and immigration (Sunder Katwala, Rob Colvile, Madeleine Sumption, and Alan Manning). Listen in, say it with me, wherever you get your podcasts. Oh and I’ll be on The Coming Storm with Gabriel Gatehouse and Lucy Proctor - doing a live show at BBC Radio Theatre tonight (fully booked, sorry!).

Three weeks to go. Three long weeks. Three weeks of doomscrolling. Of ‘unskewing polls you don’t like. Or cursing or cheering Nate Silver. Three weeks of essentially nothing changing.

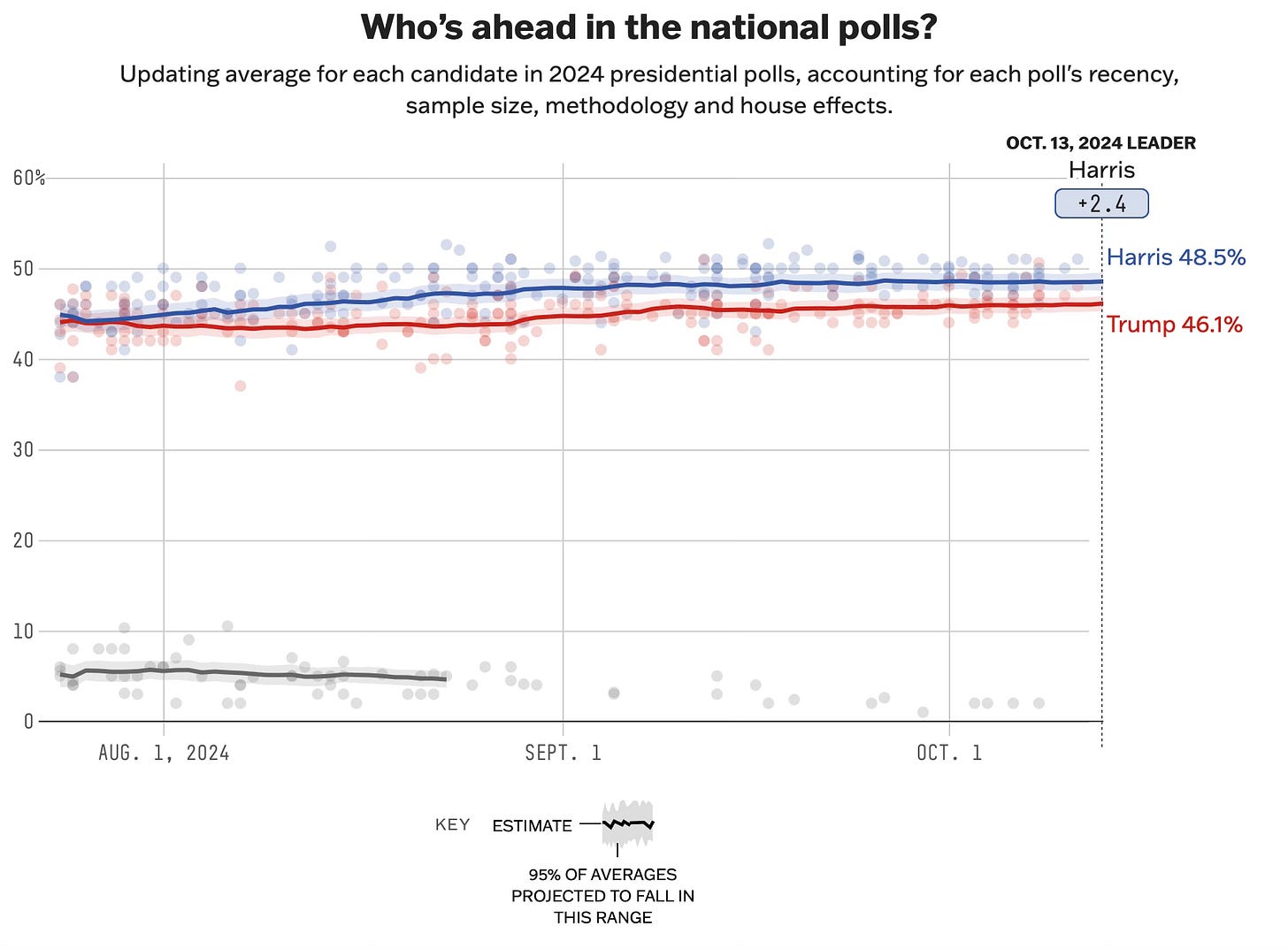
We have entered the political doldrums. The US Presidential Election has settled into stasis. Ever since early September, the national polls have been very very stable. See for example Nate Silver’s average of the polls below:

Or maybe you like the old 538?

Straight as an arrow.

Basically not very much has been happening for the last month. Really. There was a consequential-ish Presidential debate one month ago. It didn’t really do very much to the polls. There might have been some narrowing before it and then there wasn’t after but it’s all come out in the wash since then. And in the last week or so there have been signs of panic from Democrats and glee from Republicans based, as far as I can tell, some shifts in the betting markets such as Polymarket.

But aren’t betting markets predictive? Don’t they show people with ‘skin in the game’? Maybe. But remember Brexit? As polls closed on June 23rd 2016, betting markets had Remain at 90% favoured to win. That shifted to 90% Leave winning within six hours. Betting markets can be just completely off. And for American elections too. In the midterm elections just two years ago, the odds on Republicans taking back the Senate were sixty percent and rising right up to the election, even on PredictIt, which is a less MAGA-curious betting website. Part of the problem with relying on betting websites is that betting on politics is not legal in America, so the betting is being done by political hobbyist randos abroad, with all their particular peccadillos.

There is a horrible truth at the heart of the current period of the Presidential race. Nothing much is happening. It’s boring. It’s very close and things aren’t changing a lot. Yes maybe Harris is slipping slightly in Michigan and Wisconsin. It would clearly be very bad for her chances of victory if she lost them. But she is steady and maybe gaining in Pennsylvania - the biggest prize of all. And seemingly steady and rising in Nevada. It’s all basically washing out.

So we have the betting markets engaged in displacement activity because they are bored. Meanwhile the polling aggregators - Nate Silver, 538 and Split Ticket are showing nothing changing. Week after week they have Harris somewhere between a 53% probability of victory and a 57% probability. (A side note, the British pollster James Johnson, by contrast, has Trump as a probabilistic favourite over 60% - I think this relies on a lengthy series of assumptions that I am not willing to make, but perhaps he will be proven right).

Note this is the chance of winning NOT the vote share she will get (those would be huge vote shares by American standards). People who really should know better - from Elon Musk to Frank Luntz - have been getting excited about changes in probability in both the betting markets and on Nate Silver’s blog as if a percent change in the betting probability was as meaningful as a percent change in the votes of the American electorate. It is not!

Lakshya Jain had a nice visualisation of this. 55% chances of winning something is really really marginal. Can you tell if there are more red dots or blue dots in the figure below? Get your magnifying glass and tally chart out…

OK, the answer is there are more red dots. Easy right?

This is just a really really uncertain race. People need to make their peace with that. It absolutely could end up with one of the two candidates winning a landslide - and I’ll come to that below in some scenarios for after the election. But we don’t know if the polls are off systematically in favour of the Democrats (as they were in 2016 and 2020) or the Republicans (as they were in 2012 and 2022).

Just because Trump beat his polls before doesn’t mean he will this time because the pollsters have all adjusted their models. Think about it. Pollsters’ reputation is built on getting as close as possible to the final result. They are not going to all sit there and think, huh our models screwed up in the same way two times before, we will just keep them exactly the same. Nor should we worry too much about Republican pollsters ‘flooding the zone’. Bluntly, excluding or including them doesn’t make a huge difference to the race because - say it with me - it’s a really really uncertain race.

Instead, what we are probably now seeing is pollster herding because one way to try and avoid the problems of the last two Presidential elections is to weight your surveys so that they capture the voting behaviour of the respondents in 2020 (or 2016). If you have a Democrat-friendly sample in Pennsylvania but you know Biden only won it by just over one percent, then you can re-weight your participants based on their past voting. But if everyone does this, it will cause a kind of ‘shrinkage’ as everyone’s results will converge towards 2020’s results. But 2024 might be different! In terms of turnout, or voter behaviour. It’s a perfectly justifiable choice that is hard to gainsay because ultimately we just don’t know what will happen in three weeks time.

The Warm Blanket of Uncertainty

In close elections we just have to wrap ourselves in the warm blanket of uncertainty. Readers of a blog called ‘Political Calculus’ will likely be familiar with the idea of the ‘margin of error’ of a poll. It’s a statistical property that reflects the 95% confidence interval around a particular polling number.

So if you see +/- 3 percent margin of error, that means that if we randomly fielded the same survey one hundred times we would expect the level of support for an candidate in each sample to be within 3 percent points of the true level of their support 95 times out of those 100. See this great guide from Pew, who I’m paraphrasing here. That doesn’t mean you couldn’t have a really wacky survey that was five or six points away from the true level of support a candidate had - you absolutely could! It would just be in that unlucky five percent of samples that were a long way away from the real number.

The margin of error (for a 95% confidence interval) can be calculated from a relatively ‘simple’ equation, where n is the size of the sample and p is the proportion of the vote the candidate gets (equivalent to the probability a random participant supports the candidate):

\(MOE_{95\%} = 1.96*\frac{\sigma}{\sqrt{n}} = 1.96*\frac{\sqrt{p(1-p)}}{\sqrt{n}} = 1.96*\sqrt{\frac{p(1-p)}{n}}\)

If you plug in n = 1000 and p = 0.5 (a fifty-fifty election) into this formula, you get a margin of error of about 0.03 - i.e. three percent. So there’s your famous +/- 3%. Don’t say you never learn anything from this site.

If we had 3,000 respondents, we would get a smaller MOE. Something along the order of +/- 2%. If we had 10,000 a MOE of +/- 1%. At which point there wouldn’t be a great deal of point continuing to increase our sample because the benefit would be very small.

And actually the real problem might be with our sampling frame - i.e. how we create the sample, not how many people are in it. Or with our question. Or some other form of bias. So, if your surveys aren’t biased, actually only sampling 1000 people, let alone 3000, still gets you very precise results.

This is something that social scientists get really bored of explaining on Twitter - that the size of the sample can indeed be quite small and still be accurate. What you want to worry about is selection effects into the sample not its size per se. Put simply, if you have 100,000 respondents who you sampled at Trump rallies, you will get a less accurate measure than 1000 people who you random dialled from a phonebook. Unfortunately, even tech whizzes like former PayPal executive Keith Rabois don’t always seem to be aware of this…

Oops… Never mind, Keith.

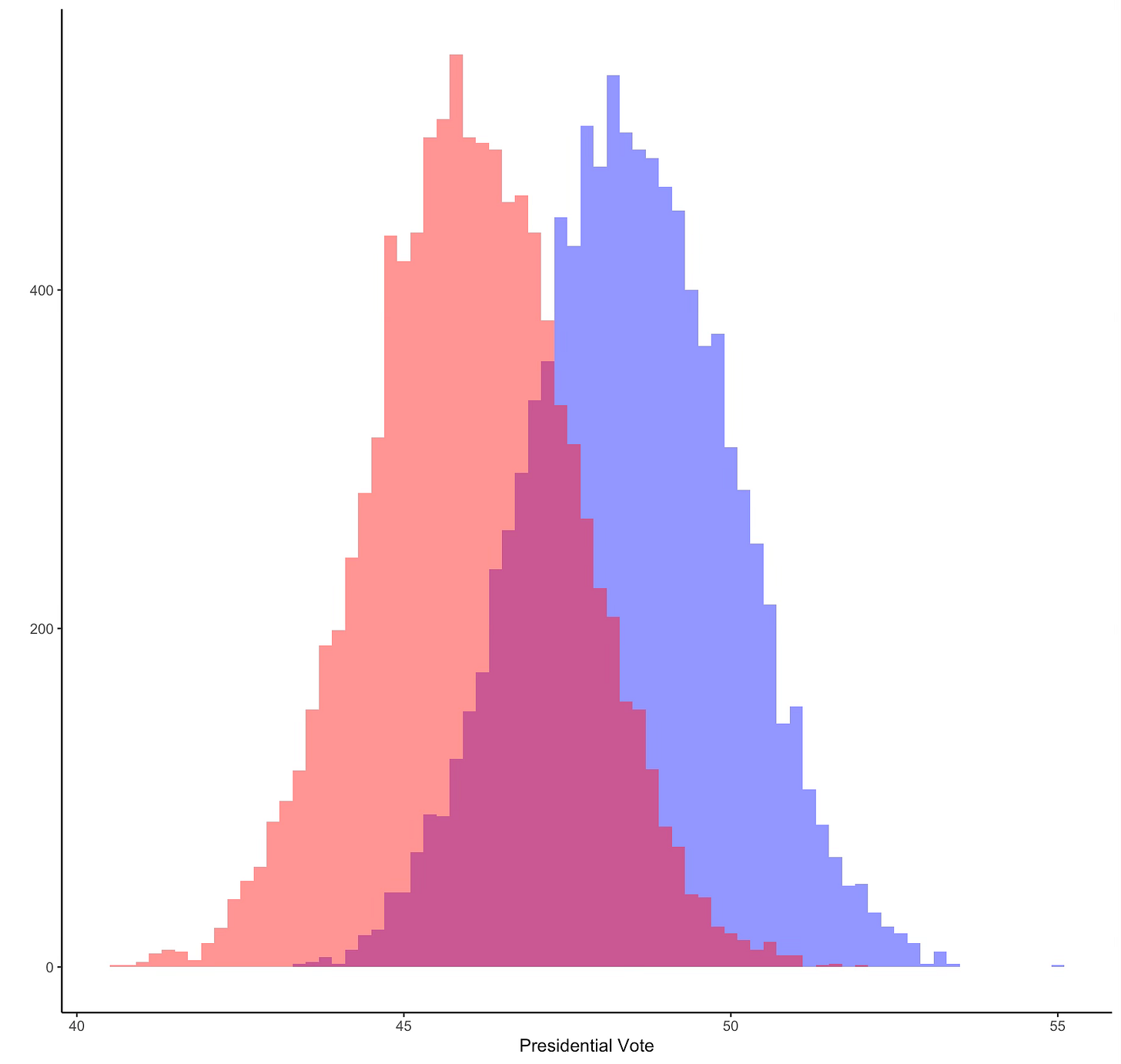
What all this mathematical fun is in aid of is to show you what that looks like over lots of potential surveys. Let’s say the 538 current polling averages are right and Harris does have 48.5% of the vote and Trump 46.1%. Imagine we kept conducting thousands of surveys, what would they look like? Like this…

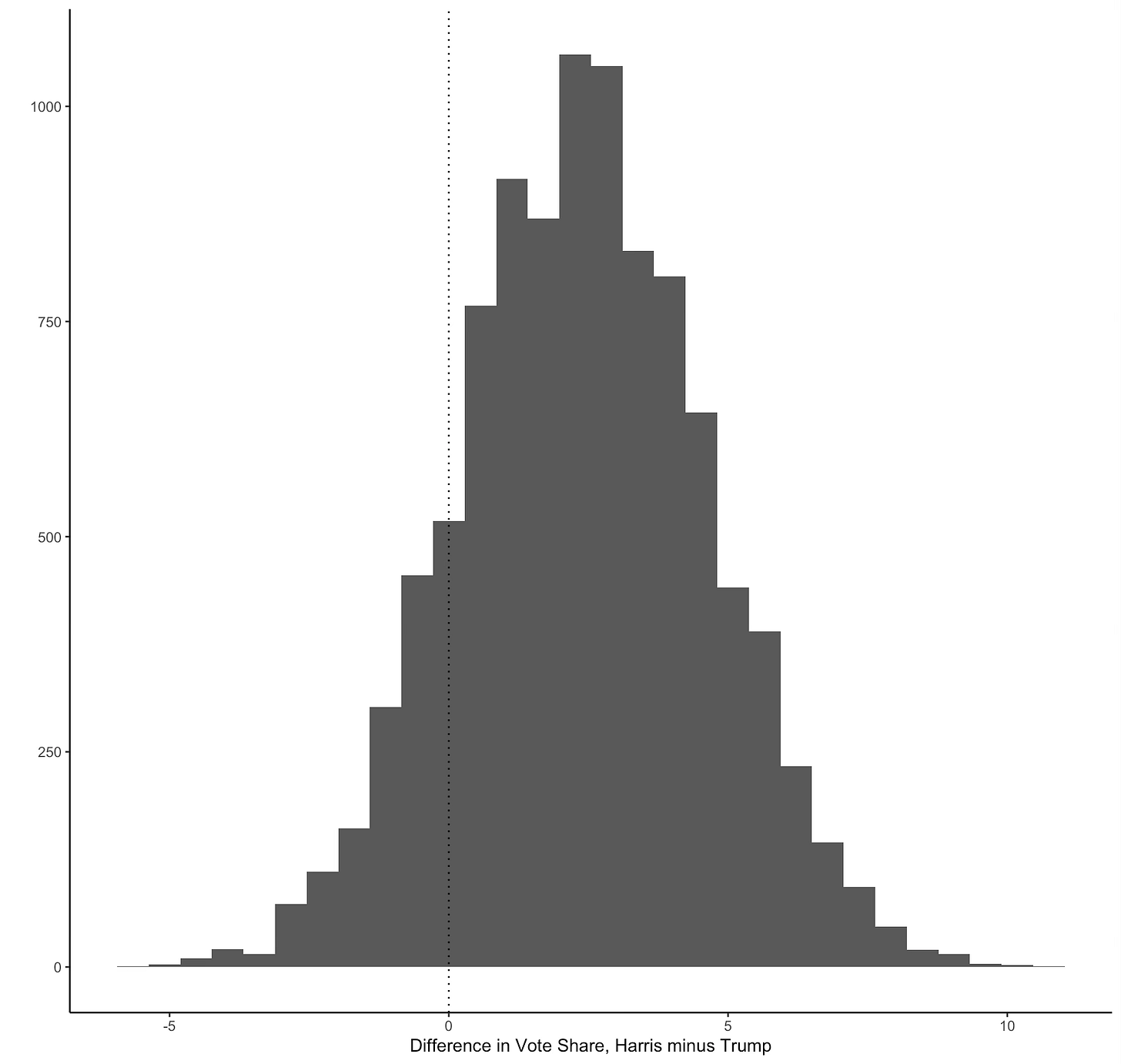
Blue is our histogram of 10,000 surveys of Kamala Harris’s support and red our histogram for Trump. Now the histograms don’t overlap completely - lots of samples have Harris with higher figures - even over 50%. But they overlap a lot. And where they overlap that means Trump would have a higher popular vote total than Harris. Now, let’s not do this too seriously since this toy model is assuming the vote shares are independent (they aren’t because there are some third party candidates and don’t knows so they are not a perfect reflection of one another and hence might be correlated). But I think what jumps out is that it is perfectly reasonable to see lots of polls with Trump beating Harris even if the true level of support is actually 48.5% to 46.1%. You can see that here when we look at the differences in support for each sample. Lots below zero.

Still, it seems unlikely that if we are getting lots of polls showing a 2.4% lead that Harris is actually behind in the popular vote. Again we need to be careful here because the graphs are produced by assuming the 2.4% lead is real but samples vary, and the last sentence proceeds in the opposite order (this is the different between likelihood and probability and I can already feel that I’m getting over my skis here). If you look at 538 for example, they find Trump wins the popular vote about 30% of the time in their simulations (which are obviously much more complex than mine).

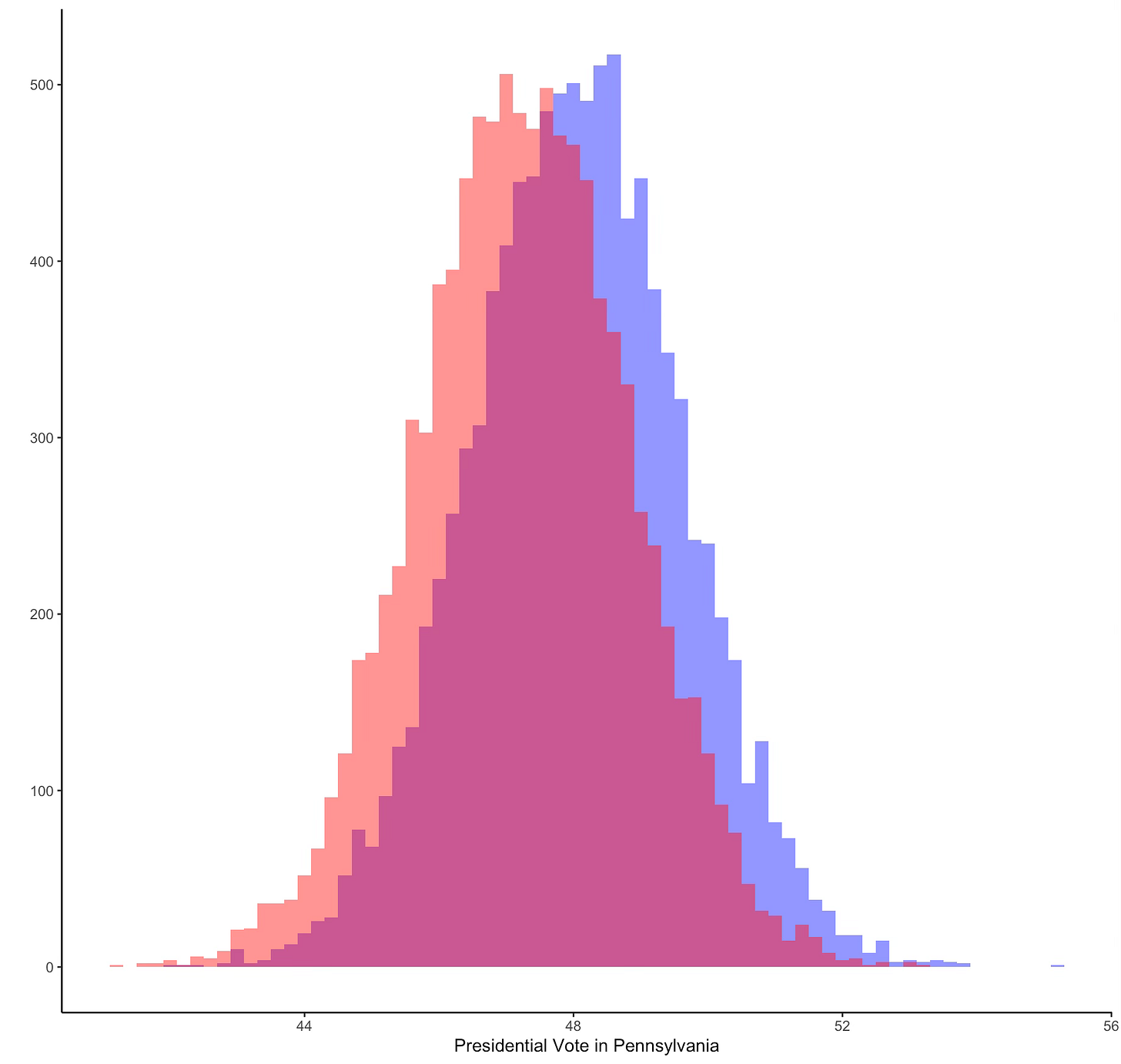
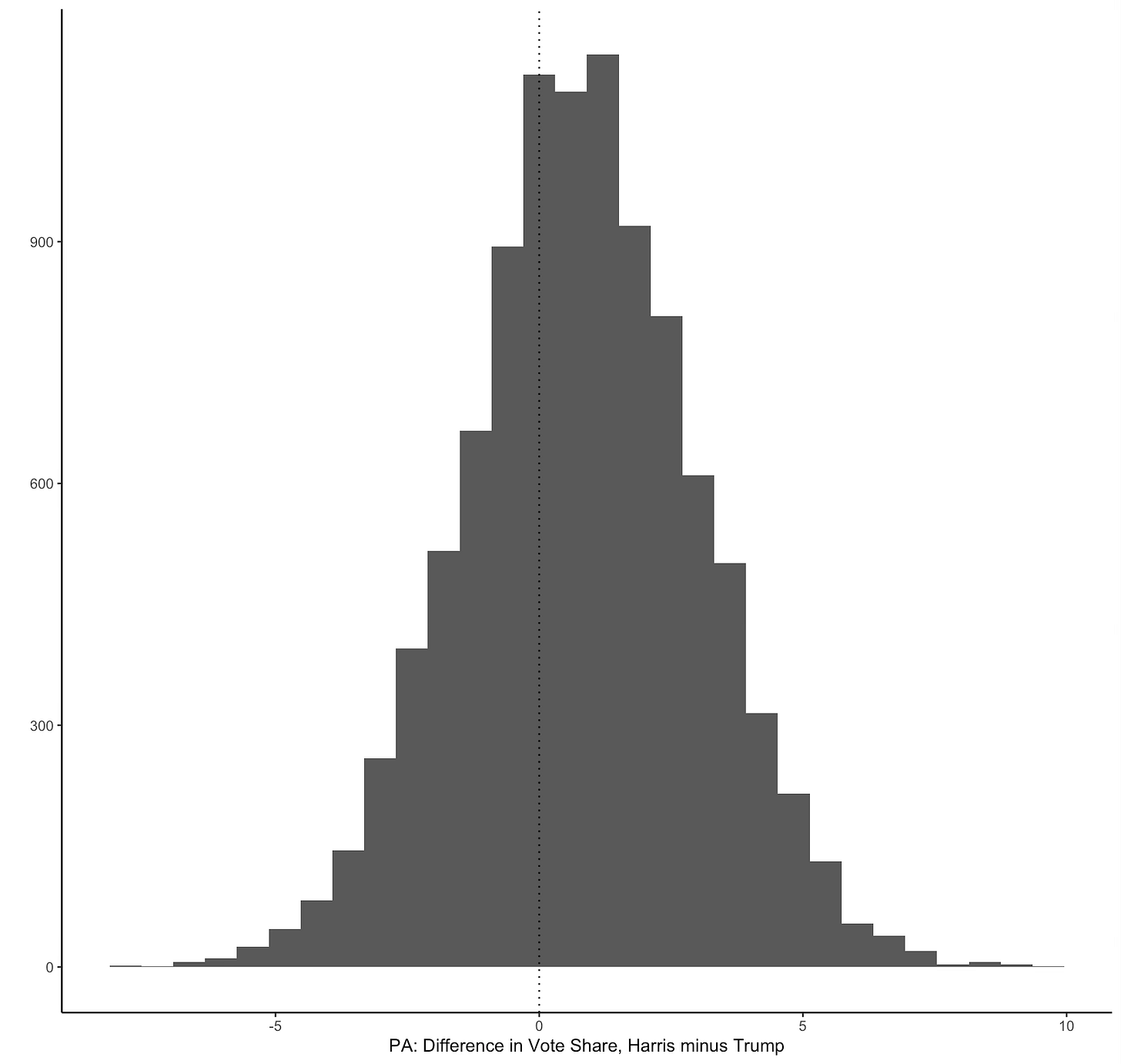
When it comes to Pennsylvania, the situation is even murkier. Again taking the current polling averages from 538 of 48.1% Harris, 47.3% Trump we get the following figures.

Who the hell knows what’s going to happen here. A ‘lead’ in average Pennsylvania polling doesn’t tell you much given how tight things are.

So we are just going to have to deal with uncertainty. Yes, I suppose it’s possible that the polls will break one way or another before the election. But they likely won’t and we will be stuck in the doldrums for three weeks. Polls, polls, everywhere and not a drop to drink.

---

Come on, give me my fix!

So what should political hobbyists be looking at? We could still look at the campaigns and the choices they are making. It suits both candidates to act as if Harris is an underdog. That’s the Harris campaign’s express strategy so a closing in of the polls - or at least panicking among Democrats as if polls were closing - might not be so bad. They are worried about complacency. Trump on the other hand does not like being cast as the underdog. Trump is, after all, allegedly a Yankees fan.

Given the candidates’ personalities and strategies it’s hard to read that much into some of their decisions about where to campaign. Yes Trump is not going to win California or New York but Trump loves to look popular everywhere so going to Coachella (or a manure farm next to Coachella) or Madison Square Garden makes sense from the perspective of the overall image he wants to give off. Similarly Harris is going with a very play-it-safe strategy of rallies in swing states, reaching non-traditional media, and avoiding traditional media in case there’s a gaffe or a question she doesn’t want to answer.

There is some alleged tea-leaf reading going on with internal polls, including various now-disgraced US media insiders claiming that Harris is having a disaster and Trump is up everywhere. I mean, maybe. But also there was an accidental leak of the Republican Senate Leadership Fund internal polls of US Senate candidates that actually looked pretty bad for Trump. So who knows?

No, I think we should cast our mind forward to November 6th. The day after the election. Because what happens in the months between then and the inauguration of the next President is going to be crucial and maybe we can game that out a little. I’ll run through four scenarios.

---

Harris Smashes It

I won’t lie, this would be my preferred outcome. I hope you can handle reading the rest of this now. I don’t think it’s enormously likely but it is quite feasible that Harris could end up with a result much like Barack Obama’s re-election, where a near-tie in the polls through election day ultimately was resolved in a four point victory and a 332-206 split in the Electoral College. Romney thought he was ahead most of the race. He didn’t even write a concession speech (though he was graceful in improvisation)!

Results in swing states tend to be correlated. Let’s say Americans just can’t stomach the idea of four more years of Trump chaos / disruption. Then it’s easy to see Harris winning five or six of the seven swing states, producing a similarish outcome such as 303 to 235. Now this is close enough to Biden’s 2020 victory that I don’t think Trump will immediately accept it. But I think the ability to forestall it would be much weaker than when he was President in 2020 or more importantly than when Mike Pence was Vice President and hence presiding for the Electoral College in January. Trump can hardly put pressure on Vice President Harris not to count the Electoral College votes in the equivalent situation.

In this case we most likely have a Democratic President and House and Republican Senate and therefore somewhat divided government not hugely different to today save with the difference that battles would be over filibusters rather than government funding bills.

Harris Squeaks It

I think this is, if I had bet my life on it, the most likely scenario. But again most likely means, very marginally more likely than the other scenarios. Remember our warm blanket of uncertainty.

I hate to tell you this but in this scenario, Donald Trump doesn’t pack up his fake tan and go home. This is actually the scenario in which having buckled up before the election makes sense, because the rollercoaster is about to drop. I categorically expect that Trump will declare that he won the election in this case and to begin legal proceedings. The Democrats have already lawyered up in advance of this. Every swing state will be litigated. Elected figures who can halt, pause, advance, etc the count will become household names, just as Katherine Harris, erstwhile Secretary of State in Florida, did in 2000.

I also think this is the case in which some form of violence is most likely. Unlike others, I suspect the violence will be sporadic, erratic and contained. I don’t think the Proud Boys will march on the Capitol and I do think the US Army would prevent any real shenanigans. But the legal debate will be under the shroud of violence - possibly in multiple partisan directions, after all, there have already been two attempted assassinations targeted at Donald Trump.

I actually think the uncertainty in this scenario is much more ‘interesting’ than the ‘warm blanket of uncertainty’ we are going through right now. Things could be very volatile and play out in unexpected ways depending on the actions of a few individuals.

However, I suspect that ultimately things in February 2025 will be stable. Harris will be President in this case and Trump will not have overturned the election. She will, however, be facing a Republican Senate and a near-tied House (probably leaning Democratic). So her ability to get much done will be much less than was the case for Joe Biden in 2021. How well she can handle that will determine how strong the forces of populism will be again in 2028 when we experience Trumpism without Trump.

Trump wins the Electoral Vote only

This is 2016 redux, only liberals feel even worse and Donald Trump feels even more vengeful. What Trump can do with that vengeance depends on what else happens. It’s not out of the realms of possibility that he wins back the Senate along with the Presidency but loses the House, which tends to mirror the popular vote for President (which in this scenario, Harris has won). If Trump doesn’t have the House then what he can do in budgetary terms is highly constrained. There will be lots of bipartisan finance conversations and certainly there will be tax cuts but perhaps not a full reshaping of the American welfare state.

On foreign policy Trump will be Trump. A popular vote loss and a Democratic House won’t affect that. So we will see the tariffs Trump has promised - likely with a series of negotiated opt-outs for favoured countries. We will see Starmer and Lammy going cap in hand for some of these, with some relief that the UK is not anymore in the EU, who are going to be Trump’s bete noire. Trump’s relations in China will be highly transactional as they were last time - with his liking for Xi’s strength moderated by his desire to look like he has won any deal. With Putin, I suspect a Trump Presidency will mean a swift end to the war in Ukraine, very much not on terms favourable to Ukraine. I can imagine that Trump would for example agree to Russia keeping troops in occupied Ukrainian provinces in return for nominal Ukrainian sovereignty or some such scam. Trump will care most about how it looks for him - so if he can sell a bad deal for Ukraine as a great deal for Trump that’s what he will do.

And what of the Democrats? A fundamental asymmetry in American politics is that the Democrats are not going to litigate the election to the extent that Trump will. If they have actually lost and they suspect they have indeed lost and everyone is telling them they have lost, they will give up. See Bush-Gore. That’s not how Trump works. He still claims he won in 2020. The Democrats will go into internal crisis mode. There will be lashing out at Biden. At Harris - for playing it safe or not safe enough. For picking Walz over Shapiro (assuming the Dems lose Pennsylvania - if they lose Wisconsin instead then who knows?). And at each other for just being the Democrats. And then they will prepare to face off against JD Vance in 2028.

Trump Makes Trump Great Again

And then there’s this. The American people give Donald Trump a huge vote of confidence and something they haven’t in two previous attempts - a popular vote lead. To be honest there was an evens chance this would have happened had Joe Biden not stepped down so we are hardly in the world of alternative history here.

Policy-wise I’m not totally sure it feels hugely different to the previous scenario with the exception that now the Republicans almost certainly have the trifecta of the House, Senate and President. And that means yuuuuge tax cuts. Trump has been promising to remove taxes on tips and overtime, and create new deductions for car loans and various business expenses. The US tax take is going be sliced. And at some point that has to mean cuts in federal spending. Though I suspect that Donald Trump does not care about federal debt. Maybe they finally axe Obamacare and replace it with Trump’s ‘concept of a plan’. I suspect they won’t fully axe Social Security and Medicare, although Trump’s voting base is not necessarily that old so I wouldn’t rule it out. Medicaid - for poorer Americans - that’s screwed.

On civil rights and immigration, this will be Trump - sorry, I mean Stephen Miller - unleashed. Expect deportation major raids to flood the news for months. Trump part 1 was caging undocumented/illegal migrants at the border. Trump part 2 would be removing people who have been in the US without papers for years, even decades. It would be very very messy and likely economically disruptive. Will it be politically unpopular? I’d like to think so but I suspect it will be divisive more than unpopular.

And then there is the really big issue (at least from over here) - Trump’s foreign policy. It will be much like I wrote above only bigger. Some people are saying it’s the biggest they’ve ever seen. There will be substantially more deference to a Trump with Reagan-like margins, including from Europe. He won’t be seen as a weird aberration produced by the Electoral College but as a political reality. As will JD Vance, whose foreign policy views are if anything more isolationist than Trump’s.

---

OK, so those are my takes. As I noted, I would prefer Kamala Harris to win. So I guess feel free to exclude my views on that basis. But I would caution people who want to claim that the election ‘leans Harris’ or (to quote James Johnson) ‘leans Trump’. I don’t see the case for making that assertion and I suspect while it’s good for engagement it’s inaccurate on any reasonable level. There is simply too much uncertainty right now to make either claim with real confidence.

And why should you trust me? Because I’m a tedious political scientist who likes to write long blogposts about how confident we should be on electoral outcomes. And I am confident about one thing - we shouldn’t be very confident one way or another. We will know soon enough.